|
BASE TEÓRICA
Esta teoría nos permite manejar y procesar
ciertos tipos de información en los cuales se manejen términos inexactos, imprecisos o subjetivos. De una manera similar a
como lo hace el cerebro humano, es posible ordenar un razonamiento basado en reglas imprecisas y en datos incompletos.
Con los conjuntos difusos(Fuzzy sets)
podemos definir sub-conjuntos, de una manera tal que cualquier elemento pueda pertenecer a ellos en diferentes grados.
Fuzzy Sets (Lofti Zadeh, 1965) - La
transición desde “pertenecer a un conjunto” hasta “no pertenecer a un conjunto” es gradual.
¿Cómo representamos un Conjunto Difuso(Fuzzy
set)?
Definición 1: Sea X una colección de
objetos, expresados de forma genérica por x. Entonces, un conjunto difuso A en X se define como un conjunto ordenado de pares
A={(c,mA(c))½cÎX},
y
mA(x)
Ejemplo: sea X = R+ las edades posibles
para un ser humano. Definimos E, sobre los 50, como
mE={(c,mE(c)½cÎC}
en
donde
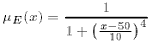
Obtenemos
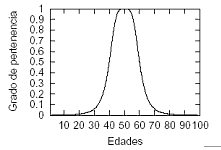
Con lo que podemos
asignar distintos grados de pertenencia.
En
la practica vamos a necesitar particionar nuestro universo.
Ejemplo:
sea X el concepto edad. Podemos particionar X usando los conjuntos.
Joven, maduro y viejo
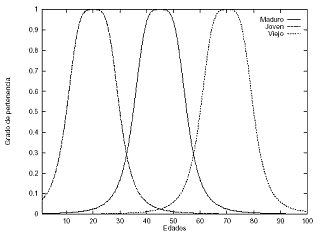
La función de pertenencia puede ser una curva
arbitraria.
Dependiendo de la aplicación y del diseñador
se pueden elegir diferentes tipos de funciones de pertenencia (“membership function”). Las más frecuentes son: triangular, trapezoidal, gausiana.

|
